道路交通騒音予測計算モデル ASJ RTN-Model 2018 の中の走行速度に関するある仕組みを発見した。
　ASJ RTN-Model 2018 の記述から基本の式を抜き出す。
　
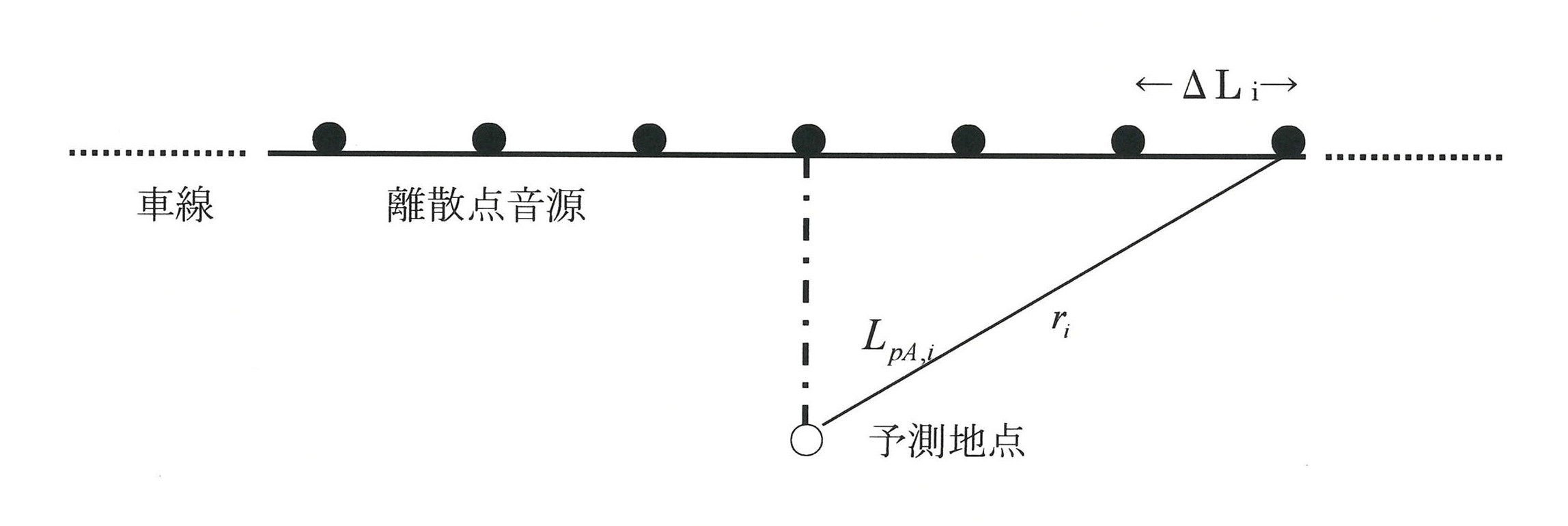
　ある予測点の騒音レベル（1個の音源区間について）
　　LA,i = LWA,i -8 -20Log(ri) +ΔLcor,i
　　i ：音源区間の番号
　　LA,i ：Ａ特性騒音レベル [dB]
　　LWA,i：Ａ特性音響パワーレベル [dB]
　　ri ：音源から予測点までの直線距離 [m]
　ΔLcor,i：各種の減衰による補正量 [dB]
　(Log は常用対数を意味する。以下同じ。)
　
　自動車走行騒音のＡ特性音響パワーレベル（1個の音源区間について）
　　LWA,i = a + bLogV +C
　　LWA,i：Ａ特性音響パワーレベル [dB]（ただし、密粒舗装道路とする）
　　V ：走行速度 [km/h]
　　a ：車種（小型車・大型車など）別の定数
　　b ：速度依存性を表す定数
　　　（ただし、定常走行区間ではb =30、非定常走行区間ではb =10）
　　C ：各種要因による補正項 [dB]
　
　単発騒音暴露レベル（1台について）
　　LAE = 10Log((1/T0)Σi(10^(LA,i/10)・Δti))
　　Δti = ΔLi/V
　　LAE ：単発騒音暴露レベル [dB]
　　T0 ：基準時間（=1s）
　　Δti ：区間iの通過時間 [s]
　　ΔLi ：区間iの長さ [s]
　 (記号^はべき乗を表す。Σiはiについての総和。以下同じ。)
　
　騒音レベル（1車線について）
　　LA = LAE + 10Log(NT/T) [dB]
　　LA ：Ａ特性騒音レベル [dB]
　　NT ：時間Tの間の交通量
　　T ：予測対象時間 [s]
　
　以上の式を書き直す。
　　LA,i = LWA,i -8 -20Log(ri) +ΔLcor,i
　　= a + bLogV +C -8 -20Log(ri) +ΔLcor,i
　　= bLogV +Ai
ただし、Vを含まない項をまとめて
　　Ai = a +C -8 -20Log(ri) +ΔLcor,i
と置いた。
　LAEの式の中の10^(LA,i/10)・Δti を変形すると、
　　10^(LA,i/10)・Δti
　　= 10^((blogV +Ai)/10)・Δti
　　= 10^((b/10)LogV)・10^(Ai/10)・Δti
ここで、
　　Δti = ΔLi/V
であるから、
　　10^(LA,i/10)・Δti
　　= V^(b/10)・10^(Ai/10)・ΔLi/V
　
　ところで、非定常走行では b=10 であるから、
　　10^(LA,i/10)・Δti
　　= V・10^(Ai/10)・ΔLi/V
　　= 10^(Ai/10)・ΔLi
すなわち、Vはキャンセルされる。LAEは
　　LAE = 10Log((1/T0)Σi(10^(LA,i/10)・Δti))
　　= 10Log((1/T0)Σi(10^(Ai/10)・ΔLi))
LAEに走行速度Vの影響はないことになり、したがって、騒音レベルに走行速度の影響はない。
市街地の一般道路のような非定常走行区間では、走行速度が変動しやすいので、騒音は走行速度に影響されないように、
巧妙にモデルが作られているということである。
（マニュアルにそのような説明は見当たらない。）
　
　一方、定常走行の場合は、 b=30 であるので、
　　10^(LA,i/10)・Δti
　　= V^(b/10)・10^(Ai/10)・ΔLi/V
　　= V^2・10^(Ai/10)・ΔLi
　　LAE = 10Log((1/T0)Σi(10^(LA,i/10)・Δti))
　　= 10Log((1/T0)Σi(V^2・10^(Ai/10)・ΔLi))
　　= 10Log(1/T0) +20LogV+10LogΣi((10^(Ai/10)・ΔLi))
したがって、騒音レベルはVの増加にともなって増加する。