道路交通騒音の計算などにおいて、遮音壁での回折の計算が必要になることが多い。
道路交通騒音のモデル計算では走行車線上に離散化した点音源を多数配置し、
各々の点音源と受音点とを遮音壁の上端を通る折れ線で結ぶ回折経路を決定することが必要になる。
折れ線の長さと点音源と受音点を結ぶ直線の長さとの差(回折経路差)が最小になる回折点の位置を決定することが必要になる。
回折経路差を表す式を回折点位置に関して偏微分して得られた式の値がゼロになる位置が最小回折経路差を与える。
この方程式は非線形であるので、数値解法により根を求める。
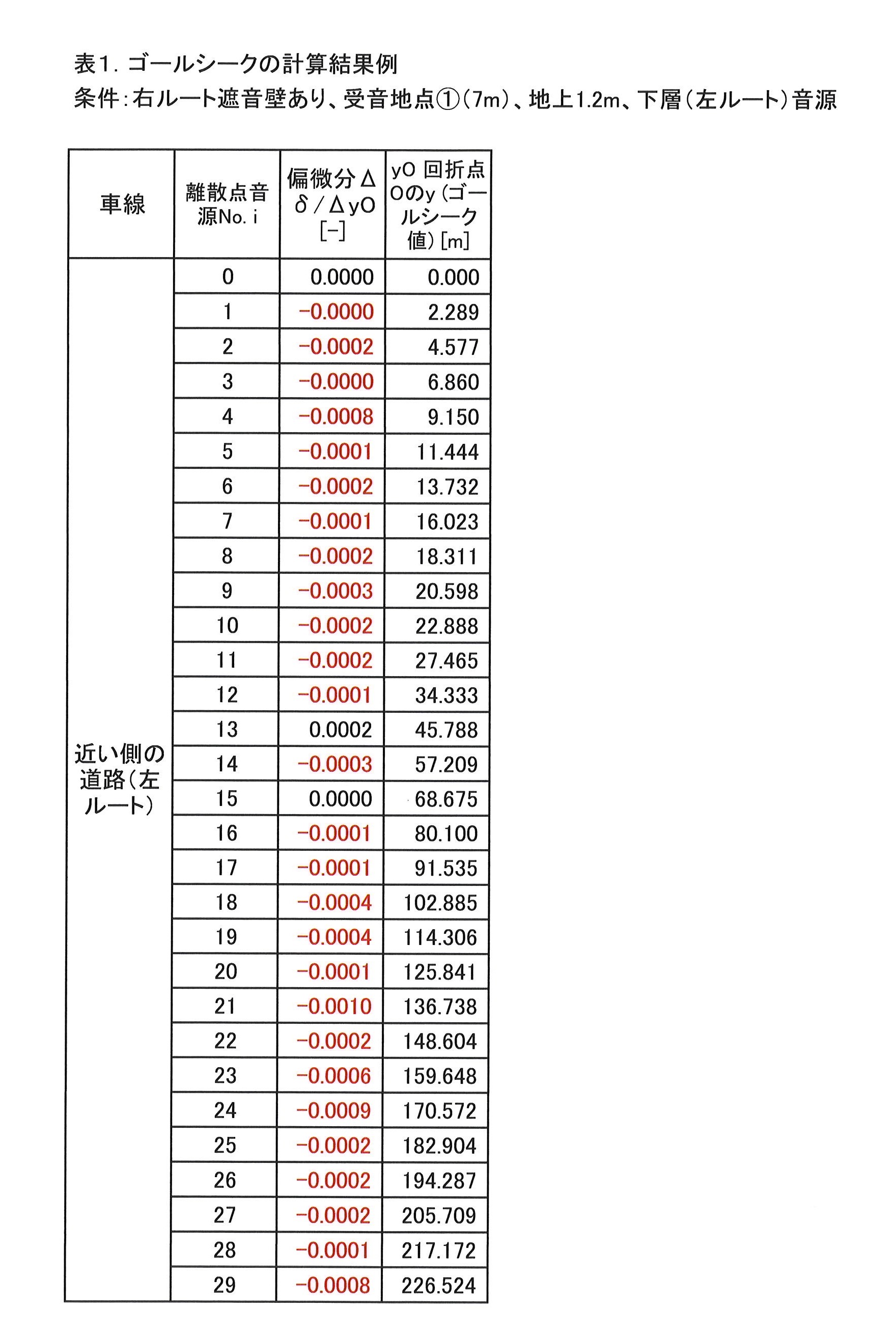
解法の一つとしてExcelの標準機能として組み込まれているゴールシーク法がある。
ただし、ゴールシーク法のアルゴリズムは公開されていないので、ブラックボックスとして利用することになる。
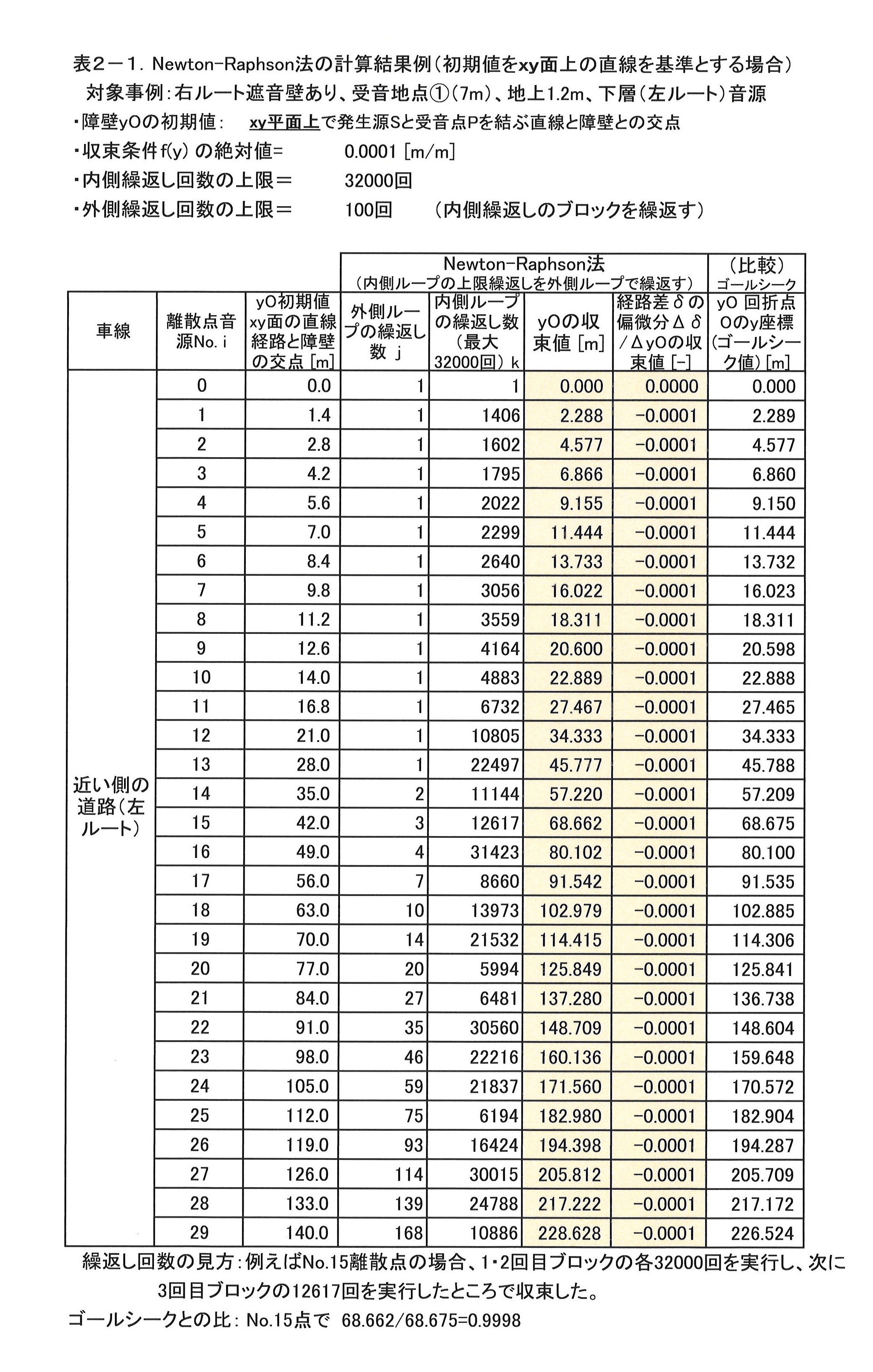
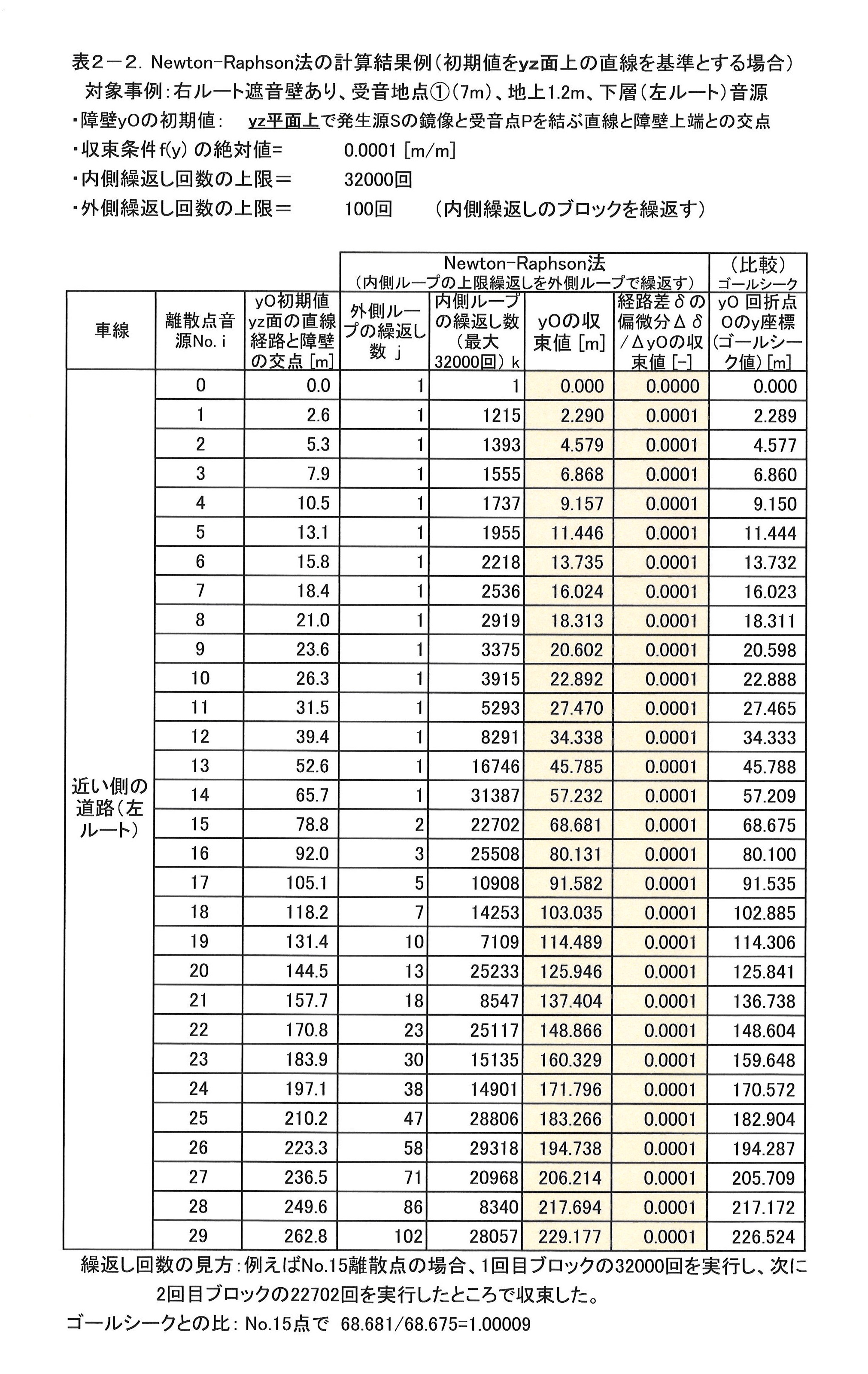
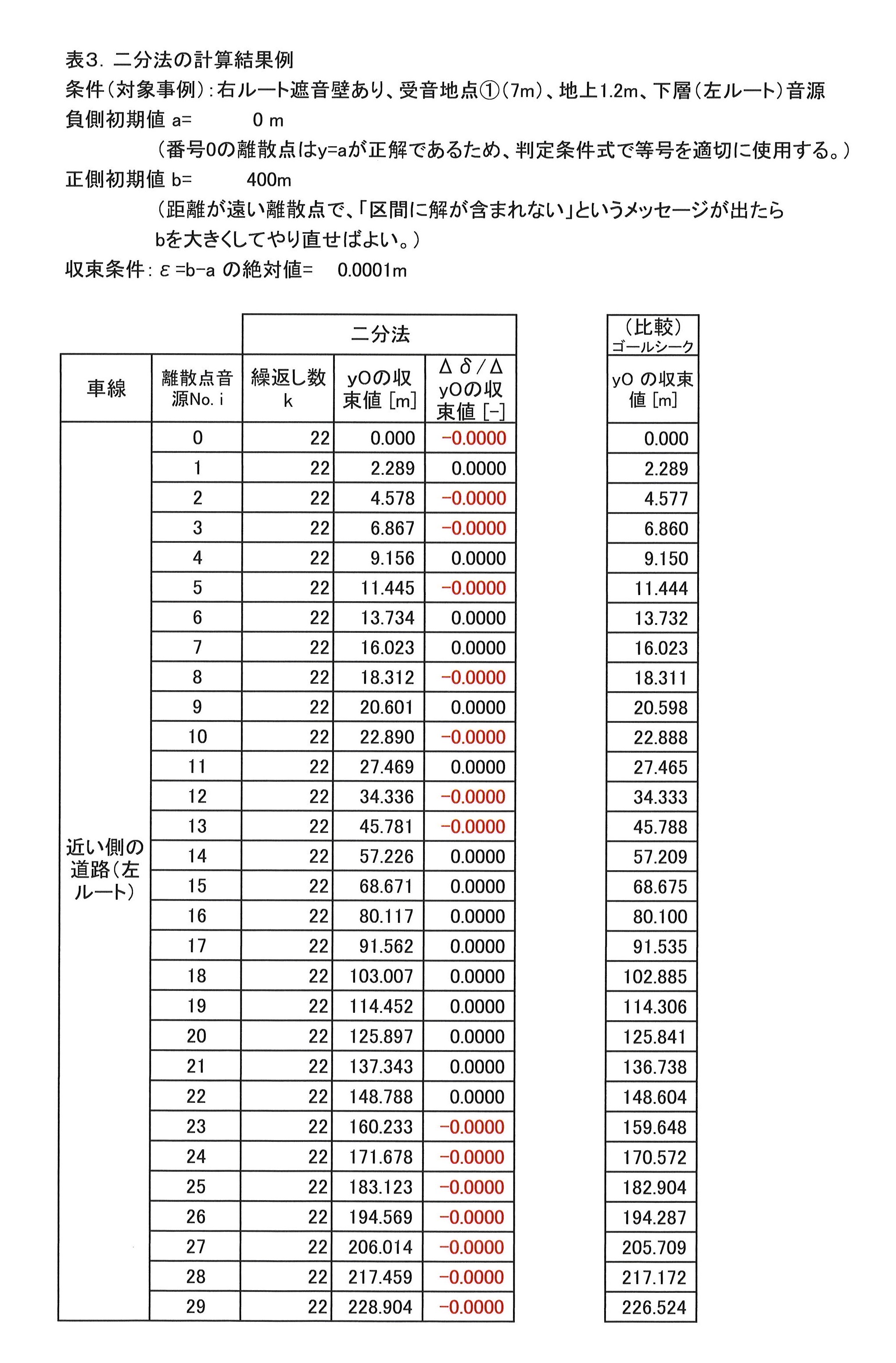
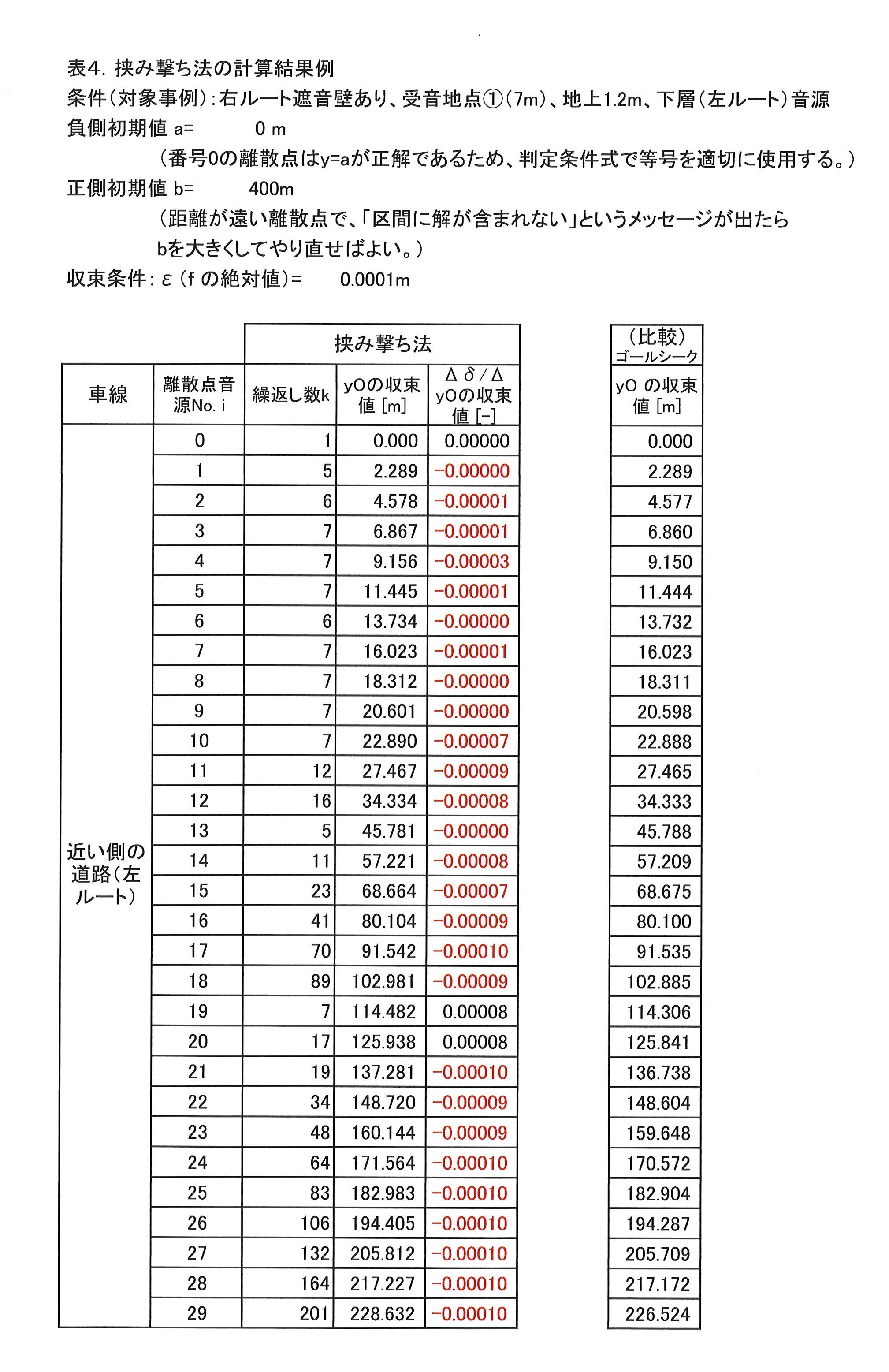
そこで、ゴールシーク法の他に、一般的に用いられる数種の解法を試して、それらの収束速度と精度を比較した。
なお適用したケースは、高架橋上を走行する車両から遮音壁を超えて地上の受音点へ達する騒音である。
| 順位 | 解法 | 特徴 |
|---|---|---|
| 1位 | ゴールシーク法 | ➀初期値を与える必要がない。 ➁収束精度を指定することができない。 |
| 2位 | 二分法 | ➀2個の区間値を与える必要がある。 ➁収束精度を指定することができる。 |
| 2位 | 挟み撃ち法 | ➀2個の区間値を与える必要がある。 ➁収束精度を指定することができる。 |
| 4位 | Newton-Raphson法 | ➀1個の初期値を適正に与える必要がある。 ➁対象関数の導関数をも与える必要がある。 ➂必要な繰り返し回数が非常に多い。 |